Modality

Most of my research to date is in modal logic (including modal type theory) and applications. This research is at the intersection of philosophy, linguistics, and type theory, so let me briefly advertise some relevance to each, to be expanded on below:

• To philosophy: I advocate a modern approach to quantified modal logic, originating in type theory, that resolves the issue of quantifying and substituting into modal contexts.
• To linguistics: I advocate a modern approach to intensional logic, which extends easily to computational and hyperintensional semantics, and is also relevant to the semantics of “scope paradox” sentences.
• To type theory: I advocate a semantics for modal dependent type theory based on morphisms of natural models (categories with families), in particular using this framework to develop the semantics of comonadic dependent type theory (c.f. Nanevski et al. 2008, Shulman 2018).

Quantified Modal and Intensional Logic

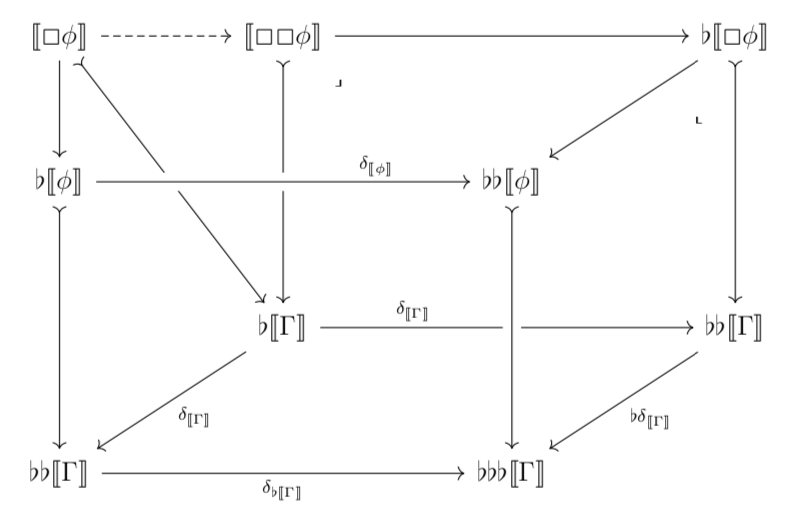
My M.S. thesis, “Montague’s Intensional Logic as Comonadic Type Theory,” develops a modern syntax and model theory for intensional logic (and, a fortiori, quantified modal logic). The syntax of the logic is based on modern approaches to modal type theory, and the model theory is based on category theory.

This approach to quantified modal logic gives a satisfying resolution to the issue of quantifying and substituting into modal contexts (slides).

In other work, I extend this approach to intensional logic to computational semantics and hyperintensional logic:

Computational Intensional Semantics

Modern type theory forms the basis for proof assistants, which can be used for computational semantics. The Agda-flat proof assistant of Andrea Vezzosi provides a setting for computational semantics subsuming both Montague semantics and type-theoretical semantics. In a paper for Mathematics of Language 2019 (paper; code), I show how to use Agda-flat to implement Montague semantics.

Underlying this application is a mode of Agda-flat, “no-flat-split”, developed by Vezzosi incorporating my feedback. With no-flat-split, Agda-flat implements a logic essentially similar to that which I have recommended for its hyperintensional properties.

Hyperintensional Logic

At Natural Language and Computer Science 2018, I discussed an approach to hyperintensional Montague semantics based on modal homotopy type theory (extended abstract; slides). Homotopy type theory has two equality notions, “definitional equality”, written ≡, and the weaker “propositional equality”, written =. This approach uses ≡ to model equality of hyperintension.

Semantics of Modal Dependent Type Theory

In my current dissertation work, I develop an approach to the semantics of modal dependent type theory, which is based on the notion of natural model (category with families). Pending my dissertation, this is discussed in my submission at Applied Category Theory 2019. In particular, I propose a notion of comonad on a natural model as the categorical semantics of comonadic dependent type theory (c.f. Nanevski et al. 2008, Shulman 2018). This notion of model is a strict (though major) generalization of the topos-theoretic semantics of modal logic given in my M.S. thesis. My pet example is the groupoid model, together with the discretization comonad. This example gives a semantics to the hyperintensional logic discussed above, and is of interest to type theorists as a model of modal type theory in which the modality does not preserve equivalences.

Other

I gave a talk at the 2018 CMU Center for Formal Epistemology workshop on a category-theoretic notion of a “2-topological space” (slides; abstract). Whereas ordinary (1-)topological spaces are models of propositional modal logic (via the McKinsey-Tarski interpretation), 2-topological spaces are models of higher-order modal logic. This work is based on Richard Garner‘s notion of ionad, but I take a 2-topological space to have an underlying groupoid of points, rather than an underlying set of points.